ビットマップによる衝突判定
概要
当記事は、2D弾幕STGにおける衝突判定をビットマップ化することで高速化できるか、という実験の報告である。
2D弾幕STGに限らず2Dゲーム全般において、余程凝らない限り、レンダリングは16ms以内に完遂される。 一方で、物体の演算は、それが複雑であったり・総数が多かったりすると、16msに収まらない場合がある。 こと衝突判定については、愚直に実装すると\(O(N^2)\)となるため、物体の数が増えるほどコストが無視できない計算となる。
しかし、単純な2D弾幕STGは「敵や敵の弾」と「自機や自機の弾」の二種類しか当たり判定を持たない。 この性質を利用して、ビットマップを用いた実質\(O(N)\)での衝突判定の性能を検証する。
ビットマップ方式
「何かと衝突した」という程度の衝突判定は、自分の当たり判定の座標に「何か」がないかを確認すればいい。 つまり、座標をkeyに「何かがあること」というvalueを得られればいい。 これに適したデータ構造は、ビットマップであろう。
衝突判定をビットマップを用いて行うのは、タイルベースゲームにおいては珍しいことではない。 ビットマップのサイズが小さく、「何かがあるか否か」という単純な真理値を持つだけでいいからである。
しかし、2D弾幕STGのような連続的な座標を取る物体の衝突判定においては、タイルベースゲーム程簡単ではない。 一ピクセルに、二次元的な当たり判定の情報を詰めなければならないからである。 愚直な実装は、ビットを内部ピクセルとする方法であろう。 しかし、後述するが、これはそれだけ多くのサンプリングを行うことに他ならず、計算量が増えてしまう。
ここで、一旦、低精度で衝突判定を行うことにして、一ピクセルにおける物体の占有率(coverage)を考える。
原理的には次の図の通りである。 自分の当たり判定がある座標のピクセルを参照し、自分の当たり判定のcoverageと相手のビットマップ上のcoverageの合計が閾値を超えているか否かで判定する。
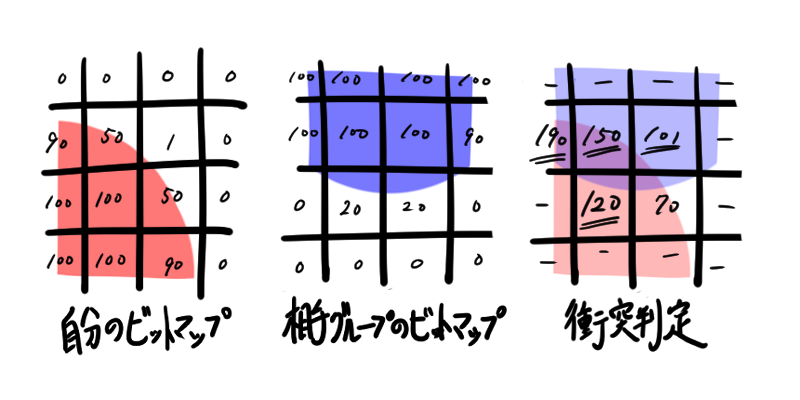
円の判定
円は、中心からの距離が一定である図形である。 こと2D弾幕STGの衝突判定においては、一般的な弾の当たり判定は円であるべきである。 （東方紅魔郷がすべての当たり判定に矩形を用いているのは、東方界隈では有名）
円での衝突判定を行うアルゴリズムは以下のようになる。
-
グループ1のすべての物体について、
- 物体の座標を更新
- グループ1のビットマップに物体のcoverageを記録
- 物体のビットマップに物体のcoverageを記録
-
グループ2のすべての物体について、
- 物体の座標を更新
- グループ2のビットマップに物体のcoverageを記録
- 物体のビットマップに物体のcoverageを記録
- グループ1のすべての物体について、物体のビットマップとグループ2のビットマップから衝突判定
- グループ2のすべての物体について、物体のビットマップとグループ1のビットマップから衝突判定
coverageの記録に三点の難点がある。
まず、物体が存在しうるピクセルのみを更新すればいいが、これを判定するのは難しい。 従って、 左を\(\lfloor x-r \rfloor\)、 右を\(\lceil x+r \rceil\)、 下を\(\lfloor y-r \rfloor\)、 上を\(\lceil y+r \rceil\) とする矩形領域内を更新領域とし、 ピクセルの中点が \(r+\sqrt{2}\)より遠ければcontinue、 \(r-\sqrt{2}\)より近ければ最大値とし、 それ以外は境界上とみなしてサンプリングを行う。
また、正方形と円が与えられたとき、共通面積を算出するのは数学的に難しい。 つまり、coverageを数学的計算によって算出することはできない。 従って、ピクセルを幾つかに分割してサンプリングを行い、その結果を総合してcoverageを概算する。
そして、グループごとのビットマップだけを比較しても、正しい衝突判定はできない。 なぜなら、ある物体が与えられたとき「coverageが0より大きい→ある物体が重なっている」は真ではないからである。 従って、物体ごとにビットマップを持つ必要がある。
以上を考慮すると、計算量は\(O(NSR^2)\)であると考えられる。 ただし、物体数を\(N\)、物体の半径を\(R\)、サンプル数を\(S\)とする。 \(SR^2\)が\(N\)に対して十分小さいとき、計算量は\(O(N)\)に見積もられる。
矩形の判定
前章の判定は、\(SR^2\)の計算量が地味に無視できないのに加え、ビットマップにアクセスするためのオーバーヘッドのためにか、実はそれほど速度が出ない。 どれほど速度が出ないかというと、\(N=1000\)の衝突判定でようやく愚直実装に追いつく程である。
そこで、conservativityを完全に無視して当たり判定を矩形にすることによって、サンプリングおよび物体ごとのビットマップを消すことにする。
矩形による判定では境界のcoverageを求めるのが容易である。次のように求める。
- 左辺：\(1-(left-\lfloor left \rfloor)\)
- 右辺：\(right-\lfloor right \rfloor\)
- 下辺：\(1-(bottom-\lfloor bottom \rfloor)\)
- 上辺：\(top-\lfloor top \rfloor\)
領域の頂点および各辺のcoverageを保存しておけば、coverageが0より大きいピクセルについて、自物体における外か内か境界上かでcoverageを場合分ければいいだけである。
計算量は\(O(NR^2)\)となる。 こちらも同様に、\(R^2\)が\(N\)に対して十分小さいとき、\(O(N)\)に見積もられる。 ただし、円の実装が各ピクセルに対して条件分岐していたのに対し、矩形の実装では走査の開始と終了のみ条件分岐を行うため、実際の計算量は円の実装より少なくなる。
結果
\(N=100, 500, 1000, 2000, 3000, 4000, 5000\)とし、それぞれ1000フレーム間物理演算を行った。 結果を線形補完したグラフを次に示す。
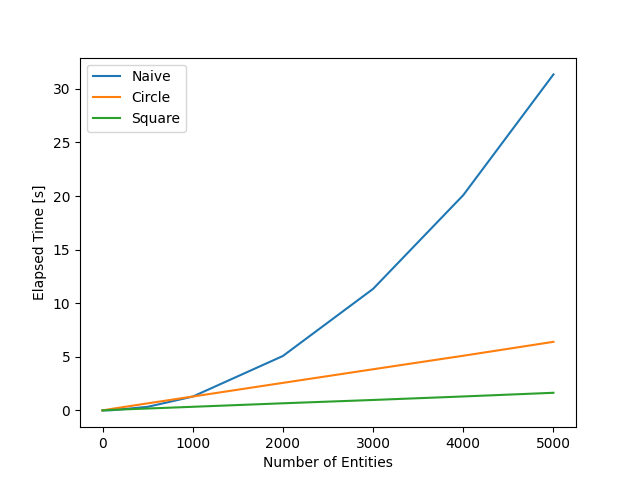
確かにビットマップ方式では\(O(N)\)となっていることがわかる。 しかし、これでは差が開きすぎていて、交差点が見えづらい。 従って、X軸の範囲を0から2000、Y軸の範囲を0から2までトリミングしたグラフを次に示す。
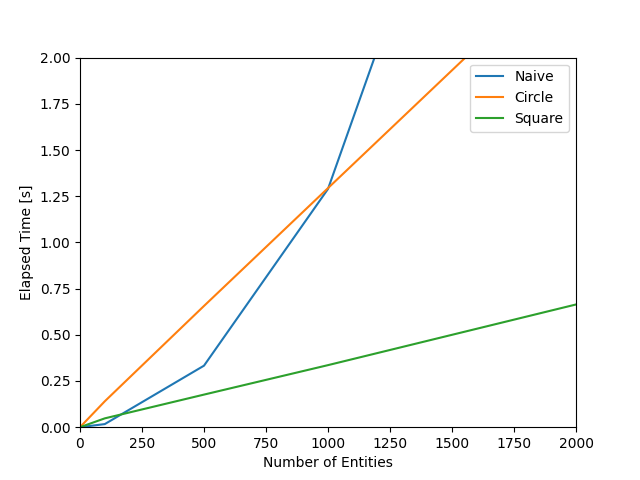
円の判定は\(N=1000\)で追いつき、矩形の判定では\(N=200\)付近で追いついていることがわかる。
結果を受けて
ビットマップ方式を使いましょう。……とはならない。 特に、矩形の判定は、conservativityを完全に無視しているため、プレイ体験を大きく損なう可能性がある。
前章のグラフは、1000フレーム間演算を行っていることを考慮すると、単位を秒からミリ秒へ読み換えれば、1フレームにかかる時間がわかる。 つまり、\(N=1000\)のとき、愚直実装と円の実装は1ミリ秒である。 ぶっちゃけ1ミリ秒なんて誤差なので、衝突判定の最適化をする理由は、実はないのかもしれない。
このことを踏まえて、どの方式を使うべきか、以下のように考えた。
- 正確な衝突判定を行いたい→愚直
- 物体の数が少ない→愚直
- \(N>2000\)となるような衝突判定を行いたい→円
- とにかく高速に衝突判定をしたい→矩形
- そもそも矩形で衝突判定をする→矩形
ところで、このビットマップ方式における当たり判定の書込みは、レンダリング処理に他ならないため、GPUで行うことで高速化する方法が考えられる。 興味が湧いたら、実装するかもしれない。
■